
|
TDCC 研究室
|

|
| HOME | ENGLISH |
卵形曲線を表す方程式を見つけた
山本 信雄
本ページの図形は、図2b 以外はすべて自由にコピーして自由にご使用できます。
(図2b だけは私の発案ではありませんのであしからず。)
|
「卵形線」の数学的な定義は Ikuro 氏のサイト
「デルトイドの幾何学(その9)」、
および、数学独学塾塾長 浅井康之氏のサイト
「塾長(校長)室」
の冒頭に書かれていますが、
ここでは、現実の鶏卵に近い形を与える曲線の方程式を追求し、
その曲線を暫定的に「卵形曲線」と呼ぶことにします。
|
|
8. 前節の高次化(その2)
|
|
1. 卵形の曲線を表す方程式の基礎的導出
卵の形は物理化学の要素を含む生理科学的な問題や進化論的淘汰の問題などが考えられますが,いわゆる卵形曲線はどのような方程式で表され得るのでしょうか。
この曲線の方程式は余りお目にかかりません。それは数学的普遍性がないからだと思います。
2021年に、(7)式への求め方について問い合わせがありました。確かに、(7)式の誘導はそれほど簡単ではないようです。それで、その誘導を参考までに、 「 (7) 式の導出」 に示します。 |
式の表示を簡単にするために, |
|
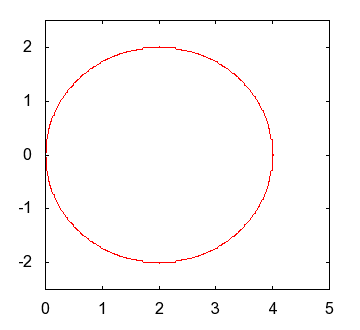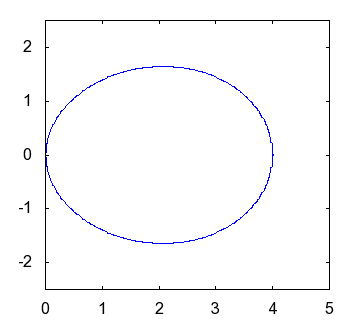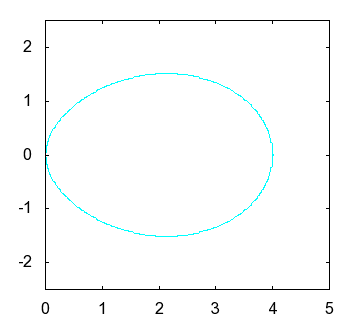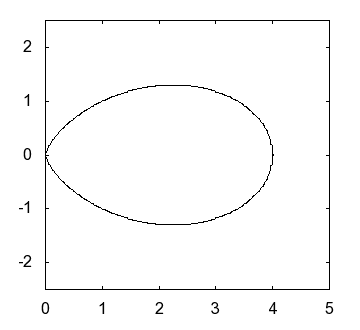
|
||
|
(ピンク色のカーブ)と現実の卵の形との比較 |
|
 . (14b)
. (14b)
|
次に、図2で示される卵形曲線の平面面積
return 2. 3次元空間における卵形の体積
|
|
となり、 b=0 のときは次式の球の体積となります。
|
 . (15b)'
. (15b)'
|
次に、卵形立体図形の表面積
(15b)式、または、(15c)式による卵形立体図形の体積 |
表1 卵形立体図形の体積
{注意1] 長径
解析的には求めることが出来ないので、Cプログラムのコンピュータ計算で求めます。
{注意2] 現実の卵に最も近いのはピンクカラーで示す
| 卵の体積 |
||||||||
| 卵の表面積 |
||||||||
周の長さ |
||||||||
平面面積 |
このうち、(15c)式による卵形立体図形の体積
return 3.
return 4. 基礎図形を円に代えて楕円とする場合
|

|
|
|

|
|
|
|
(20)式を通常の2次方程式の解法を使って解くと、
return |
|
5. 定数 a と b が定義域を外れた場合
5.1 a>0 で b<0 の場合――海栗形?
|

|
|
|

|
|
|
return
6. 卵形曲線からの一般的拡張・・・梨形曲線まで
|
|
なお、卵形曲線の(10)式の定数 c の条件は拡張の理由で解除します。定数 d と f が共に正である条件は
閉曲線を確保するためです。条件 |
 (25)
(25)
|
上式において、0 < x < a の範囲では
|
|
となります。
|
 
|
|
図8をみて分かるように、(31)式を満たさないc > 2 のときは、閉曲線が 0 < x < a の範囲外に飛び出します。また、 図9をみて分かるように、(29)式を満たさないe > 0 のときも閉曲線が 0 < x < a の範囲外に飛び出します。
また、次のような面白い図形も得られます。タマネギ形をしています。  
return 7. 前節の高次化(その1)・・・前節の圧縮図形
|
| この解は |
|
これが与える曲線の  
図13をみて分かるように、e > 0 のときは また、前節の図10、図11に相当して、次のような面白い図形も得られます。  
さらに、定数の数値を変えると、次のように、スペードの形に似てきます。  
8. 前節の高次化(その2)
 
図19をみて分かるように、e > 0 のときは
また、前々節の図10、図11、および、前節の図14、図15に相当して、次のような面白い図形も得られます。なめこに似ていますね。
 
9. 本サイトが紹介、または、引用されたサイトや文献
|
~ブラウザの「戻る」で 前に開いたページに戻ります~
~または、下のボタンを押して HOME に戻ります~
| HOME |


 , (7)
, (7)




 . (9b)
. (9b)
 , (10)
, (10)
 , (11)
, (11)
 , (13)
, (13)

 , (14a)
, (14a)
 . (14c)
. (14c)
 . (15a)
. (15a)
 , (16)
, (16)
 を求めるための C++ プログラムはこちら
を求めるための C++ プログラムはこちら
 . (18)
. (18)
 . (21)
. (21)
 . (20b)
. (20b)
 . (22b)
. (22b)

 , (28)
, (28)
 , (30)
, (30)