to this page of "Dead-Beat Effect in the LQ Optimal Control".
|
3. Block diagram of the Time Difference Comparison Compensator (TDCC)
in the case (2) used in Dead-Beat Effect of the LQ Optimal Control
The block diagram of TDCC is shown in Fig.1
in the usage of the dead-beat effect of the LQ optimal control.
As likely as in the case (1), besides the usual comparison between a desired value |
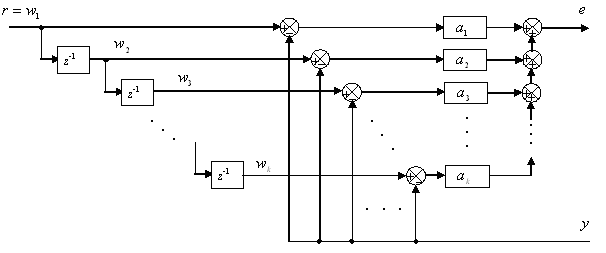
Fig.1 The block diagram of TDCC for the realization of dead-beat effect and for the degeneration
of the peak value of input variable in the ordinary LQ optimal control of digital system with a sample time
is the ratio of the direct comparison, and
are the ratios of the time difference comparisons.
is expressed as the delay element of one sample time
|
4. Application Example of TDCC for to simultaneous effects of both dead-beat and suppression of the peak value of manipulation variable
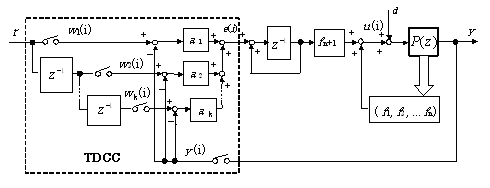
We introduce the LQ optimal control system with TDCC as shown in Fig.2. In precise, please see reference (1) and/or reference (2) described below [If you click this column, the thesis in PDF files will appear] and references (3)-(6).
In Fig.2, |
|
| Fig.2 Brock diagram of LQ optimal control system with the use of TDCC in digital design |
|
|
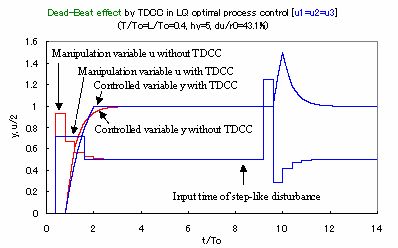
Fig.3 Simultaneous effects of both dead-beat and suppression of the peak
value of manipulation variable by TDCC in the system shown in Fig.2 Response of disturbance is not influenced by the existence of the TDCC. |
|
5. References and patents about TDCC in account of
simultaneous effects of a dead-beat control and the degeneration of the peak value of the input variable
(1) Nobuo YAMAMOTO, Michiya MASUDA, Akinori KAWAHARA, Takaya TANABE, and Makoto KIKUCHI: Dead-Beat Effect in LQ Optimal Control with the Use of Time-Difference Comparison Compensation, Research Reports of Ibaraki National College of Technology, No.41, pp.31-38 (2006).
6. Postscript
An invitation mail from the WMSCI 2005 Organizing Committee of Journal of Systemics, Cybernetics and Informatics, to participate in the 9th World Multi-Conference on Systemics, Cybernetics and Informatics, which will take place in Orlando, Florida, USA, from July 10-13, 2005, with respect to our research was arrived at February 23, 2005.
|
and a controlled variable 
,
and the controlled valuable 
(where 
) respectively.
Then, the total of these multiplied ones is derived as renewal deviation error 
which will be inputted to the usual controller for LQ optimal control in a feedback loop.
Standing on the TDCC mentioned above,
indicates the transfer function of a plant in digital expression.
In Fig.3, we show indicial responses of both of the controlled variable 
, comparing between two cases with and without TDCC each other.
From these result, it is appear that both the dead-beat effect and the suppression effect of the peak value of the manipulation variable 
does not change in the existence of the TDCC.