1. Preface
Napier's constant is widely known as having an especial value as like as Euler's constant.
Napier's constant performs the main role expressing linear natural phenomena.
The reason stands on the characteristics that the derivative of exponential function is the exponential one itself.
In this page, we intend that some foundation of its reason is made clear in respect to both the algebraic ultimate-value's expression of the Napier's constant
and the analytic treatment of the exponential function.
[Notice] Euler's constant is given in the following;
 ,
where ,
where
 . .
2. Original differential equation and its solution
The original simple differential equation which is composed of two continuous functions of
 and and  in all range of in all range of  is assumed to be given as in the following;
is assumed to be given as in the following;
 , (1) , (1)
where the sign ( ) represents derivatives.
The solution of Eq.(1) is given in the case of ) represents derivatives.
The solution of Eq.(1) is given in the case of  as as
 , (2) , (2)
and in the case of  as as
 , (3) , (3)
where  and and  are integration constants. are integration constants.
As Eq.(2) is thought to be related to Eq.(3) in respect to the continuity in the neighborhood of  ,
the relation between the two constants must be as the following; ,
the relation between the two constants must be as the following;
 . (4) . (4)
If we take the ultimate value of Eq.(2) at  in the case of in the case of  ,
we obtain that ,
we obtain that
 , (5) , (5)
where we take
  .
(6) .
(6)
Another approach from  also reaches the same result although imaginary values should be treated. also reaches the same result although imaginary values should be treated.
Thus, it is recognized that the solution of Eq.(2) in the limit of  exists only in the case of
exists only in the case of  from Eq.(5).
This fact may be thought to be the origin of the exponential function. from Eq.(5).
This fact may be thought to be the origin of the exponential function.
3. Algebraic and analytic expressions of exponential function
The special case of  in Eq.(5) will be treated in the foregoing description.
According to such a treatment, Eq.(5) must coincide to Eq.(3).
So, the following equation can be described. in Eq.(5) will be treated in the foregoing description.
According to such a treatment, Eq.(5) must coincide to Eq.(3).
So, the following equation can be described.
 , (7) , (7)
where  is considered from Eq.(4) as is considered from Eq.(4) as  . .
Another expression of Eq.(7) is written as
 . (8) . (8)
If we take the expansion series of powers in the right-hand side of Eq.(7), we obtain that
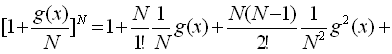  . (9) . (9)
Furthermore, in the case of  , Eq.(7) is led to , Eq.(7) is led to
 . (10) . (10)
Thus, the Taylor's expansion is derived as Eq.(10) certainly.
4. Conclusion
Although we have obtained the Eq.(7) which connects the algebraic and the analytic expressions of exponential function,
the calculation process mentioned above is hardly seen.
However, this process will find a side of the essence of the exponential function.
[A problem]
As the Napier's, the Euler's and pi's constants are given by  , ,
 and and  respectively,
then, the following equation is calculated.
Although the three constants is thought to have no relation each other,
the value of the equation closely coincides to a unit by 0.11 percent error. respectively,
then, the following equation is calculated.
Although the three constants is thought to have no relation each other,
the value of the equation closely coincides to a unit by 0.11 percent error.
 ,
(11) ,
(11)
Though such a coincidence is thought to be accidental,
how is such a close coincidence interpreted mathematically, meaningless or not?
[Reference] Another relation has been found as below.
But, the value of this equation have the error of 0.98 percent more than the above one.
 .
(12) .
(12)
[The other approximation]
Although the following equation is also made by a numerical value adjustment,
the value of the equation closely coincides to the Napier's natural constant  by 0.037 percent error. by 0.037 percent error.
 .
(13) .
(13)
|

 . (8)
. (8)
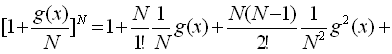
 . (9)
. (9)
 . (10)
. (10)
 .
(13)
.
(13)