|
ここに3個の方程式があります。
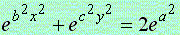 ,
(1) ,
(1)
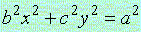 ,
(2) ,
(2)
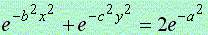 ,
(3) ,
(3)
ただし、(1)式と(2)式の定数 a, b, および, c は任意の実数ですが、
(3)式の定数 a のみ次式の制限があります。
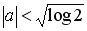 .
(4) .
(4)
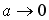 のとき、(1)式と(3)式の双方共マクローリン展開によって(2)式に移行することが次の計算で示されます。 のとき、(1)式と(3)式の双方共マクローリン展開によって(2)式に移行することが次の計算で示されます。
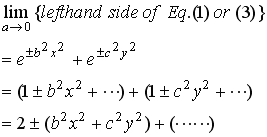 .
(5) .
(5)
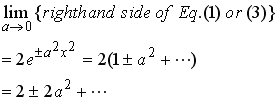 .
(6) .
(6)
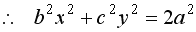 .
(7) .
(7)
このように移行した(7)式は、その式の性格が(1)式と(3)式のそれと連続しているとみなされる一方で、
(1)式と(3)式から独立したとして考えられるので、改めて、(7)式右辺の
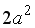 から係数の 2 を取り去って(2)式のように書き換えることは自由です。
(式の全体的な概要さえ変更になっていなければ問題ない。) こうして、(2)式の a, b, および, c を任意の実数と再定義できます。 から係数の 2 を取り去って(2)式のように書き換えることは自由です。
(式の全体的な概要さえ変更になっていなければ問題ない。) こうして、(2)式の a, b, および, c を任意の実数と再定義できます。
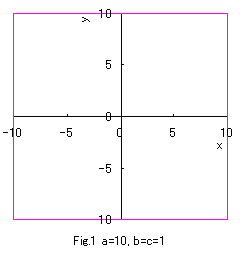
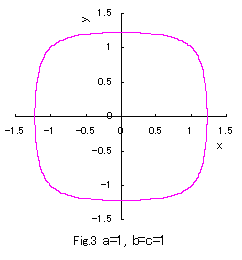
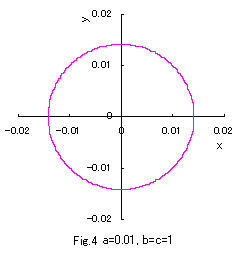
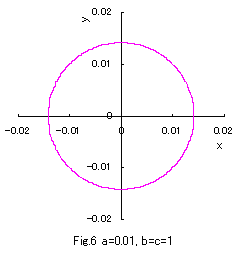
b=c=1 の場合につき a の値をいろいろ変えて、(1)式、(2)式、および、(3)式をコンピュータで計算させてグラフに表しますと,
図1から図10 のようになります。
(1)式は凸形に歪んだ円、(2)式は円、(3)式は凹形に歪んだ円を表示し、
(1)式において a の値が十分大きいときは四辺形となり、
(3)式において a の値が定義域最小のときアステロイド曲線(星形曲線)に似てきます。
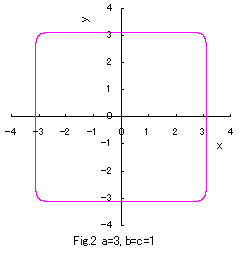
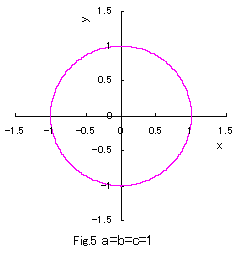
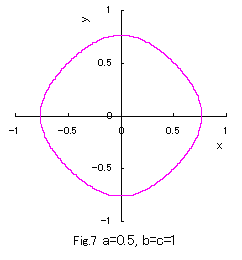
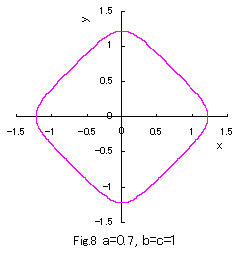
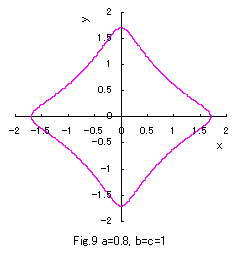
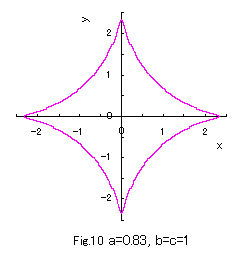
|
上図をアニメーションで示しますと次のようです。
なお、画像の自動切り替え方法はこちら
 (アーカイブ版)を参考にしました。 (アーカイブ版)を参考にしました。
|
(1)式において a の値が十分大きいとき、b と c の値を変えることによって、
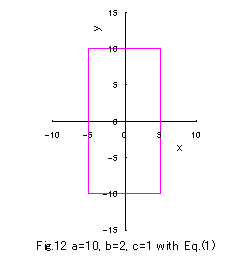
別方法のこちら  と同様に、縦と横の長さが異なる矩形(長方形)が得られます。a=10 で、b=1, c=2 の場合と b=2,
c=1 の場合の2例を次に示します。
と同様に、縦と横の長さが異なる矩形(長方形)が得られます。a=10 で、b=1, c=2 の場合と b=2,
c=1 の場合の2例を次に示します。
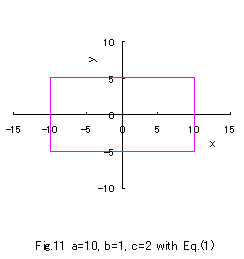
[参考]
一般的方法
一般的には、次の方程式によって円や楕円、および、凹凸双方の歪んだ円または楕円が表現できます。
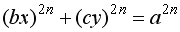 ,
(8) ,
(8)
n=4 の場合と n=1/4 の場合の2例を次に示します。
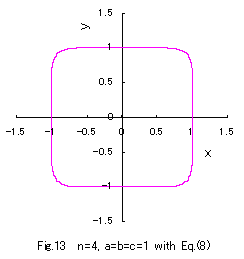
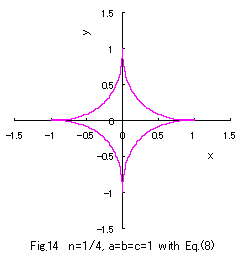
次数 n が自然数とその逆数のときは計算が容易ですが、それ以外の広い範囲では数値計算がやや面倒です。
けれども、 n を限りなくゼロに近づけることが可能なので、
本文の方法において(4)式の制限を受ける図10 の星形よりも、図14 のように、より鋭い星形を表現できる強みがあります。
|

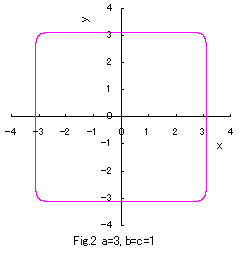


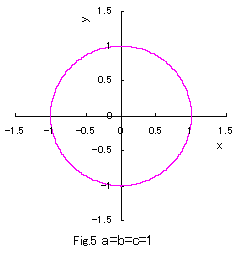

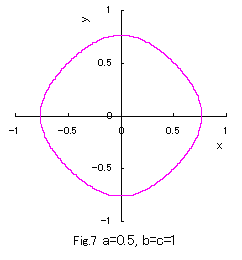
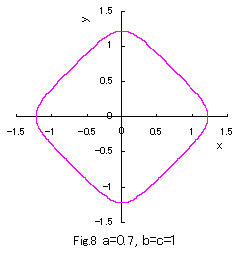
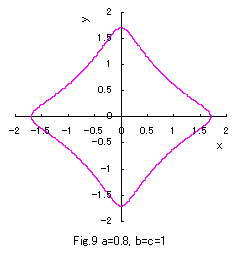
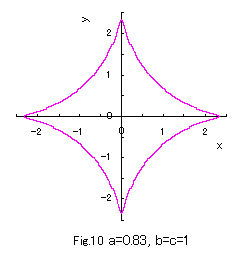
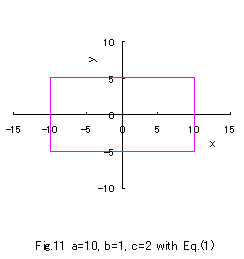



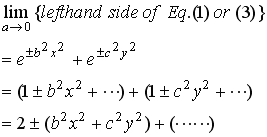 .
(5)
.
(5)
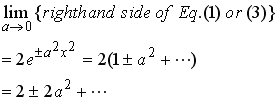 .
(6)
.
(6)